MIDACO:Mixed Integer Distributed Ant Colony Optimization
MIDACO-SOLVERは、単目的および多目的最適化問題を解くための高性能数理ソフトウェアです。もともとは、欧州宇宙機関(ESA)[3]、[7]、Astrium(2013年よりエアバスグループ)[7]において、宇宙開発の現場で生まれる難易度の高い混合整数非線形計画法(MINLP)問題のために開発されました。その後、
MIDACOは、目的関数 f(x) が連続変数または整数変数、あるいはその両方の変数 x をとる問題(混合整数問題)を扱います。さらに、等式制約および/または不等式制約 g(x) を含む問題にも対応します。以下、MIDACO が扱う最適化問題を説明します。
最適化問題

ブラックボックス最適化ソルバーであるMIDACOは、目的関数f(x)と制約関数g(x)が明示的な数式で与えられる必要はありません。決定変数xが与えられると、MIDACOが必要とするのは目的関数と制約関数の数値的な値を返すことだけです。これらの目的関数と制約関数の値の計算は、MIDACOとは完全に独立しているため、ブラックボックス内で行われると見なされます。このブラックボックスの概念により、ユーザーは検討する事例の表現と定式化において、最大限の自由を得ることができます。特にMIDACOは、非線形性、非滑らかさ、非凸性、微分不可能性などが高い問題関数を持つ問題の求解が可能です。さらに、中程度の確率的ノイズを含む問題も、MIDACOは確実に解くことができます。
アルゴリズム
MIDACOは進化アルゴリズムであるアントコロニー最適化(Ant Colony Optimization, ACO)に基づいています。特に、MIDACOは連続変数を扱うACOを実装しており、混合整数を含む探索領域に拡張されています(詳細は[1]または[6]の第2章を参照)。下の図は、連続変数の場合(左)と整数変数の場合(右)について、この混合整数拡張ACOが、多重カーネル確率密度関数(PDF)を用いて決定変数の探索空間をサンプリングする様子を示しています。
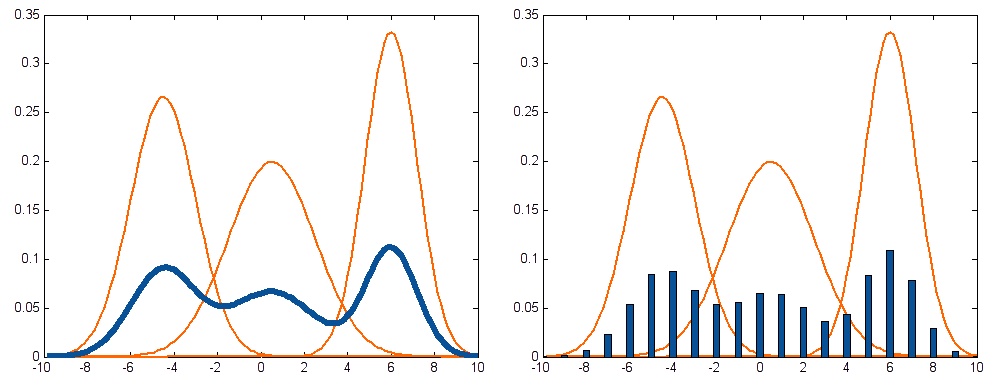
MIDACOでは、制約条件がオラクルペナルティ法▷(Oracle Penalty Method)によって処理されます。これは進化アルゴリズムが大域最適解に到達するための高度で自己適応的な手法です。すべての進化アルゴリズムと同様に、MIDACOも大域最適解への到達を保証するわけではありませんが、何百ものベンチマークでの広範な数値テスト([5]および[17]参照)により、ほとんどの問題において迅速かつ確実に大域最適解を得る能力が実証されています。特に[5]では、既存の古典的なMINLPアルゴリズム(例えば、分枝限定法)に対して、大域最適化の能力と実行時間の点でMIDACOが優位にあることが示されています。
MIDACOの背後には、複雑な実世界での利用において、無理のない時間で妥当な良解へと最適化できる堅牢なアルゴリズムを提供したい、という想いがあります。全体的な性能を向上させるために、MIDACOは多くのヒューリスティックやアルゴリズムを実装しており、迅速な局所収束のための疑似勾配法に基づくバックトラッキング直線探索も含まれています。そのため、MIDACOは進化的ハイブリッドアルゴリズムに分類されます。
ソフトウェア
10年以上にわたって開発・改良されてきたMIDACOソフトウェアは、MINLP、制約付きおよび大規模最適化における進化計算の最先端を代表しています。このソフトウェアは、スタンドアロンでの使用だけでなく、外部のアルゴリズムやソフトウェアへの統合(組み込み▷)も想定しています。MIDACOは、利用しやすいインターフェースと最高レベルの計算効率の両立を目指しています。また、超軽量(約200KB以下)のANSI-CまたはFortranのソースコードとして提供されるMIDACOは、完全に独立して利用可能であり、ウェブサーバーやマイクロプロセッサーを含む、すべてのプラットフォーム(Windows/Mac/Linux)上でポータブルにコンパイル・実行が可能です。さらに、Excel、VBA、C#、Java、R、Matlab、Python、およびJuliaなど、人気言語へのゲートウェイも提供されています。MIDACOソフトウェアは、10万個の変数、数千個の制約条件、および数百個の目的関数を持つ問題にまでスケールアップすることに成功しています。
MIDACOソフトウェアの特別な機能として、複数の解候補を並行して評価する並列化オプションがあります。並列化により、数値シミュレーションなどのCPU時間を要する事例の計算時間(経過実時間)を大幅に短縮することができます([17]を参照)。
MIDACOの並列化アプローチには、2つの大きな強みがあります。第一の強みは、特定の言語やアプローチに限定されず、事実上あらゆる言語やアプローチで実現できることです。現在の並列化テンプレートには、例えば OpenMP、MPI、GPGPU、Apache Spark、Fork/Join、マルチプロセッシング、mpi4py などが含まれます。第二の強みは、MIDACOの内部アルゴリズムコンポーネント(例えば、集団サイズ)やCPUハードウェア仕様に依存せずに、並列化係数を自由に選択できることです。これにより、MIDACOはあらゆる分散HPCシステムに高度に適応し、大規模な並列化を利用できるようになります。
ユーザーと利用事例
MIDACOは、世界中の学術機関や企業で何百ものユーザー▷にライセンスされています。 MIDACOの利用事例▷の範囲は幅広く、自動車産業、化学工学、通信、ロボティクス、土木工学、電気工学、バイオテクノロジー、気候、エネルギー、金融など、さまざまな分野に及びます。特に、MIDACOは(航空)宇宙工学の分野で広く利用されており、例えば、欧州宇宙機関(ESA)、ドイツ航空宇宙センター(DLR)、日本宇宙航空研究開発機構(JAXA)、韓国航空宇宙研究院(KARI)のほか、Astos Solutions、MT Aerospace、Almatech、PACE Aerospace、三菱重工業などの航空宇宙関連産業で使用されています。 MIDACOの最もエキサイティングな利用事例の一つは、惑星間宇宙ミッションの軌道設計であり(例えば[7]、[12]、[13]、[14]、[18]を参照)、この分野でMIDACOはいくつかの最適解記録を保持しています。
※[*]の文献については参考文献のページをご覧ください
※詳細はユーザーマニュアルをご覧ください

