宇宙ミッションでの利用事例
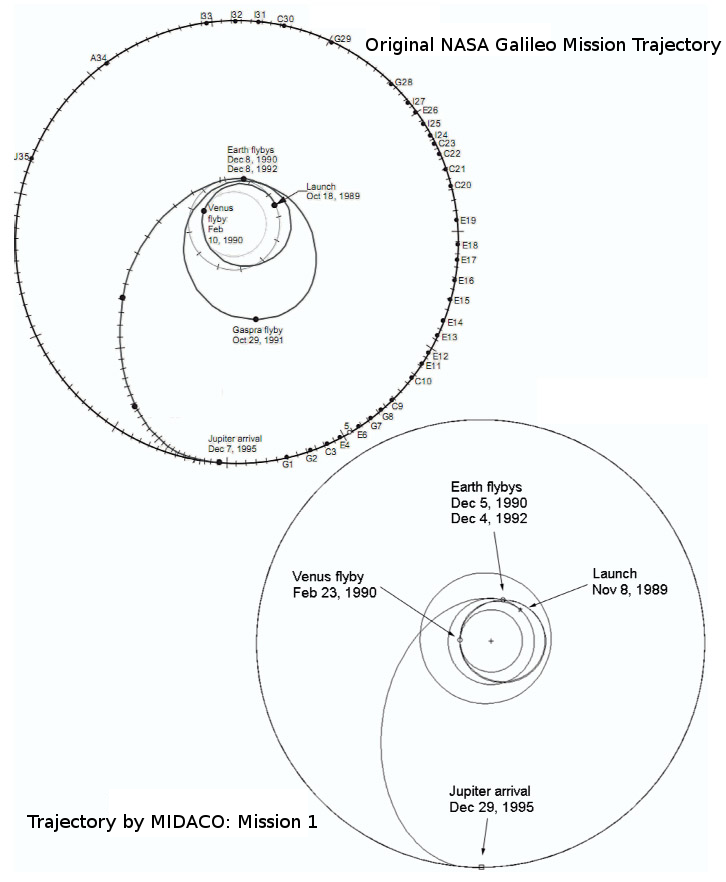
下記の参考文献[1](第4章)では、地球から木星への惑星間宇宙探査の軌道をMIDACOを用いて計算しました。本軌道モデルは、1989年にNASAが打ち上げたガリレオミッションをもとに作成されています。この宇宙探査モデルの実装は、バーミンガム大学(Rueckmann J、Schlueter M)、ミュンヘン連邦軍大学(Gerdts M)、欧州宇宙機関(ESA)、およびEADSアストリアム(AIRBUS)(Kemble S)との共同作業によるものです。
| NASAガリレオ探査機(実機) | ガリレオミッション(イメージ) |
 |  |
ここで検討されるミッションモデルは、多重重力アシスト(MGAまたはフライバイ)および深宇宙マニューバ(DSM)軌道に分類されます。MGA-DSMの最適制御問題は困難であることが知られており(GTOPXデータベースを参照)、通常は単純な連続最適化問題として扱われますが、MIDACOの性能を活用することで、ミッションモデルを混合整数領域に拡張することが可能となりました。MIDACOでは、連続制御パラメータ(打ち上げ日、フライバイの高度、推力の方向など)に加えて、潜在的なフライバイ惑星(金星、地球、火星…、冥王星)も、カテゴリ型整数変数(金星=1、地球=2、火星=3など)で表現することにより自動的に選択されます。このような混合整数最適化問題への拡大は、ミッションモデルの求解をかなり困難にしますが、探索空間が大幅に広がるほか、宇宙エンジニアが事前にフライバイ惑星を手動で選択する手間を省くことができます。
| | ガリレオミッション | MIDACOミッション1 | MIDACOミッション4 |
| 打ち上げ日 | 1989年10月18日 | 1989年11月8日 | 1989年7月6日 |
| 第1回フライバイ | 金星 | 金星 | 金星 |
| 年月日 | 1990年2月10日 | 1990年2月23日 | 1990年1月21日 |
| 第2回フライバイ | 地球 | 地球 | 地球 |
| 年月日 | 1990年12月8日 | 1990年12月5日 | 1990年9月4日 |
| 第3回フライバイ | 地球 | 地球 | 火星 |
| 年月日 | 1992年12月8日 | 1990年12月4日 | 1990年12月21日 |
| 総所要期間 | 6.14 年 | 6.14 年 | 4.15 年 |
| Delta V | 不明 | 3.350 m/sec | 5.177 m/sec |
結果的にMIDACOは、地球から木星までのさまざまな実行可能MGA-DSM軌道を自動的に生成することができました。MIDACOが計算したDelta(Δ)V(宇宙船の推進力を表す)が最も小さい軌道は、元のガリレオミッションと非常によく似ており、同じ特性(および同じフライバイ惑星!)を有しています。MIDACOミッション4は、全体の期間が約2年短くなる代替ミッションですが、その達成にはかなり多くの推進力を必要とします。
参考文献
| [1] | MIDACO on MINLP Space Applications | JASR (Elsevier) Vol 51(7), 1116–1131 (2013) | Preprint |
| "Defense & Aerospace Week"誌掲載のレビュー論文は こちら |
| JASR journalによる論文へのレフェリーコメントは こちら |