MIDACOによる制約条件の処理について
オラクルペナルティ法
オラクルペナルティ法は、進化的およびメタヒューリスティック最適化アルゴリズムのための高度な制約処理アプローチです。この方法は、その予測的な性質のためにオラクルと呼ばれる単一のパラメータ「オメガ(Ω)」に基づいています。このパラメータは、大域最適目的関数値f(x)に直接対応します。ユーザーが大域最適f(x)値について何らかの(大まかな)推測値を持つような、実世界での事例の場合、この情報をオラクル情報として活用すると、最適化アルゴリズムの収束速度を向上させることができます。ユーザーがこうした情報を利用できない場合は、無限大(∞)の値から開始して、より良い(実行可能な)解が見つかった場合にΩを更新する(自動)更新ルールを適用できます。
自動更新機能を持つオラクルペナルティ法を実装したアルゴリズムは、自己調整型(self-tuning)に分類されます。オラクルペナルティ法の適用例として、アリコロニー最適化(ACO)については[1]、[6]、[7]、[15]、[17]、遺伝的アルゴリズム(GA)については [2]、[10]、[11]、粒子群最適化(PSO)については[3]と[16]、人工蜂コロニーアルゴリズムについては[12]、微分進化(Differential Evolution 、DE)については[4]、[5]、[8]、[13]を参照してください。またオラクルペナルティ法は、決定論的方法にも拡張されました[14]。この方法に関する最も詳しい紹介は[1]に、キーコンセプトにある目的の簡単な説明はこちらのPDF ▶(スライド11-15)にあります。MIDACOが数百の(非線形)制約を持つ問題を迅速かつ堅牢に解決できる主要な理由の一つが、オラクルペナルティ法なのです(ベンチマークを参照)。
オラクルペナルティ関数の数式
( Section 2.3 ▶ )

Omega = 0の拡張オラクルペナルティ法のグラフ
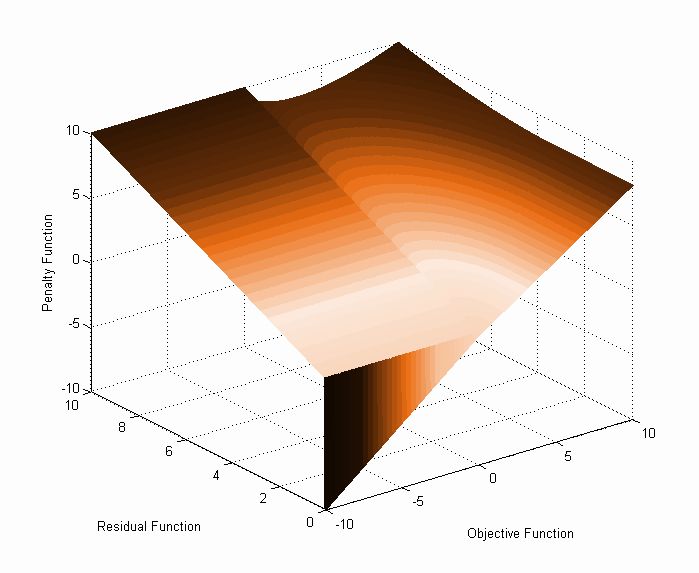
| ソースコード | ||
| Matlab | ▼ oracle_penalty.m ▼ | LaTeX formula ▼ oracle_penalty.tex plot_oracle_penalty.m |
| C/C++ | ▶ oracle_penalty.cpp ▶ | |
| Fortran | ▼ oracle_penalty.f ▼ | |
参考文献
| [1] | Schlueter, Gerdts | The Oracle Penalty Method | Journal of Global Optimization (Springer), Vol. 47, Issue 2, Pages 293-325 (Preprint) (2010) |
| [2] | Munawar et al. | Advanced genetic algorithm to solve MINLP problems over GPU | IEEE Congress on Evolutionary Computation CEC, pp. 318 - 325 (link) (2011) |
| [3] | Dong, Cheng, Niu | A Constrained Particle Swarm Optimization Algorithm with Oracle Penalty Method | Applied Mechanics and Material (AMM) pp. 303-306, 1519 (2013) |
| [4] | Dong, Wang, Cheng, Jiang | Composite differential evolution with modified oracle penalty method for constrained optimization problems | Mathematical Problems in Engineering, Vol. 1, pp. 1-15, DOI:10.1155/2014/617905 (Paper) (2014) |
| [5] | Dong, Cheng, Niu | Adaptive Constrained Differential Evolution Algorithms based on Oracle Penalty Function | Computer Applications and Software (Chinese), DOI:10.3969/j.issn.1000-386x.2014.01.078 (2014) |
| [6] | Gebreslassie, Diwekar | Efficient ant colony optimization for computer aided molecular design: case study solvent selection problem | Computers & Chemical Engineering (Elsevier) Volume 78, Pages 1–9 (2015) |
| [7] | Gebreslassie, Diwekar | Efficient ant colony optimization (EACO) algorithm for deterministic optimization | Int. J. Swarm Intel. Evol. Comput. 5:131. doi:10.4172/2090-4908.1000131 (link) (2016) |
| [8] | Chen, Liang | An Optimization Approach of SRM Sphere Slot Grain Design Based on Improved Differential Evolution Algorithm | Advanced Materials Research, Vol 971-973, Pages 1072-1075 (2014) |
| [9] | Gago-Vargas et al. | Nonlinear integer problems with applications to engineering design | Computational Optimization and Applications (Springer), http://dx.doi.org/10.1007/s10589-015-9739-3 (Preprint) (2015) |
| [10] | Sato, Watanabe, Igarashi | Multimaterial Topology Optimization of Electric Machines Based on Normalized Gaussian Network | IEEE Transaction on Magnetics, Vol. 51, No. 3, Art. 7202604 (Preprint) (2015) |
| [11] | Noguera | What's New in DiscoverSim Version 2 | INFORMS 2015 Workshop, Philadelphia USA (PPTX) (2015) |
| [12] | Zhang, Han, Wang | Emulsion Explosive Formulation Optimization Based on Hybrid Artificial Bee Colony Algorithm | Acta Analysis Functionalis Applicata, Vol.17, No.4, pp. 421-430 (Preprint) (2015) |
| [13] | Shi, Liu, Feng, Zhao | Improved Differential Evolution Based PA Energy Efficiency Optimization Scheme with Joint Polarization-QAM in OFDM Systems | IEEE/CIC International Conference on Communications in China (ICCC), DOI: 10.1109/ICCChina.2017.8330407 (link) (2017) |
| [14] | Costa, Rocha, Fernandes | A Penalty Approach for Solving Nonsmooth and Nonconvex MINLP Problems | Springer Proceedings in Mathematics & Statistics, vol 223.doi.org/10.1007/978-3-319-71583-4_4 (link) (2018) |
| [15] | Paffrath, Zhou, Guo, Ertl | Interactive winding geometry design of power transformers | IEEE/ICOA, 4th Inter. Conf. on Opt. App., DOI: 10.1109/ICOA.2018.8370494 (link) (2018) |
| [16] | Zhengtonga, Zhengqi, Xiaokui, Chen | Multimaterial layout optimization of truss structures via an improved particle swarm optimization algorithm | Computers & Structures, Vol. 222, pp 10-24 (Elsevier) (2019) |
| [17] | Acciarini | Solar Sailing Polar Mission to the Sun | Master Thesis, TU-Delft, Netherlands (link) (2019) |
| [18] | Sato, Igarashi | Automatic Design of PM Motor Using Monte Carlo Tree Search | IEEE Transaction on Magnetics,DOI: 10.1109/TMAG.2022.3164926, (link) (2022) |
| [19] | Otomo, Sato, Ken, Onozaka, Hajime | Parameter and Topology Optimizations for Wireless Power Transfer Device | IEEE Transactions on Magnetics,DOI: 10.1109/TMAG.2023.3301995 (link) (2023) |
